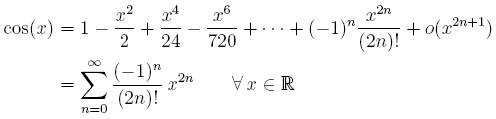
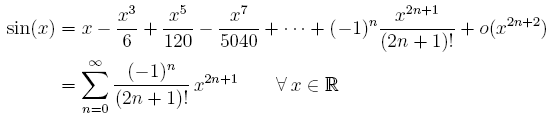
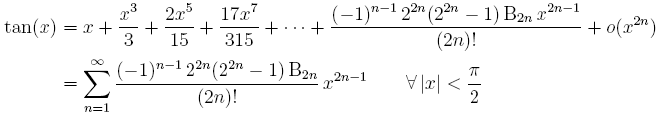.
Nous allons nous intéresser dans cette activité à la méthode qu'utilisent les calculatrices pour calculer les fonctions trigonométriques.
Contrairement à l'opinion commune, la grande majorité des calculatrices et des logiciels de calcul formel n'utilisent ni développement en série ni approximation polynomiale pour calculer les fonctions trigonométriques.
Rappelons avant toute chose les développements en séries entières de Taylor des fonctions trigonométriques :
.
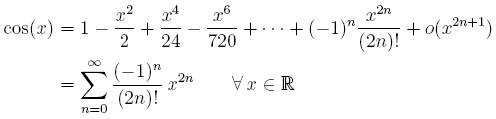
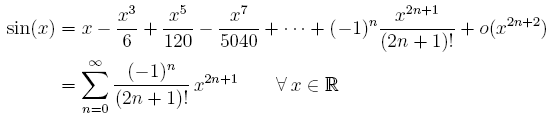
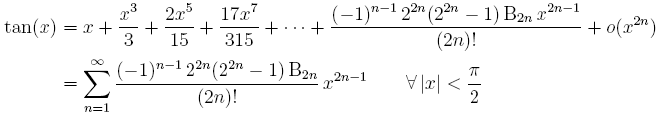La série de Taylor de la fonction tangente est plus compliquée que celle des fonctions cosinus et sinus puisque les nombres de Bernoulli Bk interviennent dans le calcul des coefficients cherchés ; à partir de n = 3, le n-ième nombre impair de Bernoulli est nul. À ce propos, les premiers nombres de Bernoulli sont :
.
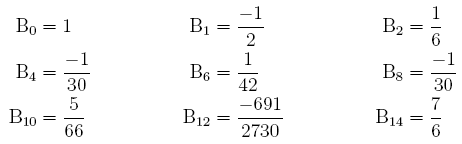Bien que l'on puisse utiliser les formules de Taylor – convergentes – qui donnent par ailleurs de très bonnes approximations, cette technique est évitée car elle nécessite un grand nombre de multiplications assez coûteuses en temps. C'est pourquoi l'algorithme CORDIC – acronyme de COordinate Rotation DIgital Computer –, développé par Jack Volder en 1959, est préféré. L'idée remonterait cependant au mathématicien anglais Henri Briggs (1561-1630), l'un des inventeurs du logarithme décimal, encore appelé « logarithme briggsien ».
Une synthèse très intéressante consacrée à l'architecture CORDIC sur les calculatrices de poches est accessible sur une page rédigée par feu Jacques Laporte (ayons une pensée pour lui).
Comme son nom l'indique, l'idée de l'algorithme CORDIC est de calculer tan(θ) en faisant subir à un vecteur de coordonnées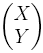 
des rotations d'angles de plus en plus petits, tendant vers 0, et dont la somme est égale à θ. Le quotient 
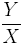est alors clairement une approximation de tan(θ) par définition de la tangente.
Considérons un angle θ tel que ![theta dans ]0; pi/2[](/maths/trigo/calcul/cordic/images/theta-ineg.png)
et une suite décroissante de θk, c'est-à-dire telle que 
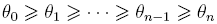, avec 
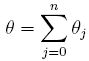, où n est un entier naturel.
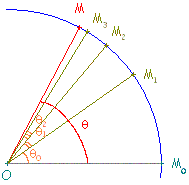
Soit le point M0 de coordonnées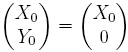 
. Alors le point M1, image de M0 par la rotation de centre O et d'angle θ0, a pour coordonnées 
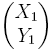vérifiant :
.
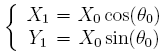En effet, si l'on identifie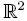 
au plan complexe d'Argand-Cauchy et que l'on utilise alors les affixes des points dans ce plan, M0(z0) a pour image M1(z1) avec z1 défini grâce aux formules de transformation de coordonnées par rotation pure :
.
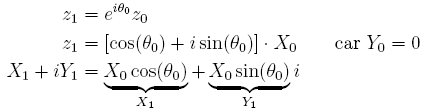Démontrons maintenant par récurrence sur l'entier k que :
.
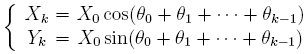On a vu le résultat pour k = 1. Le résultat est d'ailleurs aussi valable pour k = 0 étant donné qu'une somme d'aucun élément est l'élément neutre 0, d'où le résultat avec cos(0) = 1 et sin(0) = 0.
Soit maintenant k > 1. Si l'on note zk-1 et zk les affixes respectives de Mk-1 et de Mk, et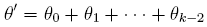 
, Mk est le transformé de Mk-1 par la rotation de centre O et d'angle θk-1. D'où la relation :
.
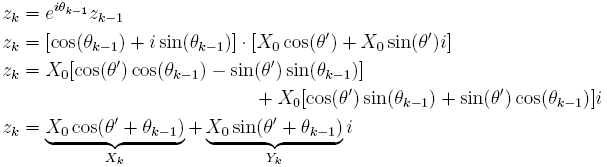On a donc démontré le résultat annoncé par récurrence.
Remarquons alors que :
.
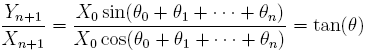Ainsi, tan(θ) ne dépend pas de la coordonnée X0 initiale. On pourra donc prendre X0 = 1 dans un premier temps. Et comme 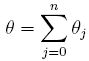, il suffit de calculer les n+1 coordonnées des points Mk afin d'obtenir la valeur de tan(θ). Or, pour calculer ces coordonnées, il suffit de savoir calculer les cos(θk) et les sin(θk), ce que nous ne savons pas faire puisque l'algorithme sert précisément à pouvoir les calculer ! L'astuce consiste à transformer nos relations sur les affixes des points de manière à faire apparaître des tangentes.
On a donc :
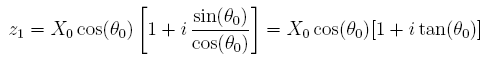
et l'on montre par récurrence sur l'entier k que :
.
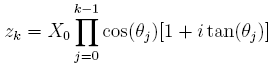En effet, par hypothèse de récurrence, on peut écrire :
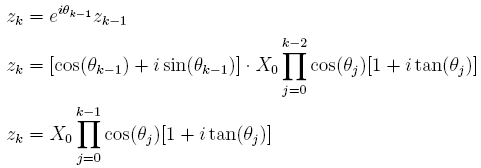
si bien que, par simplification dans les coordonnées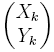 
obtenues, il ne reste plus que le rapport de la partie imaginaire sur la partie réelle de l'expression :
.
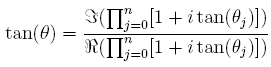Cette relation ne fait intervenir plus que les tan(θk). Pour calculer tan(θ), il suffit donc de savoir calculer les tan(θk).
Par conséquent, il s'agit de choisir les tan(θk) judicieusement. Nous allons en fait prendre les θk de manière à ce que tan(θk) = 10-k. Dès lors, le passage de Mk à Mk+1 s'obtient uniquement à l'aide de calculs très élémentaires puisque :
.
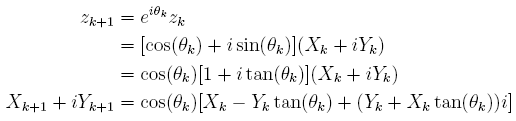D'où les relations simples :
.
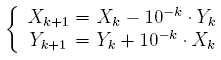De tels calculs sont extrêmement rapides à mettre en œuvre informatiquement étant donné qu'ils ne nécessitent que des additions, des soustractions et de simples décalages de virgules.
Il faut cependant avoir préalablement en mémoire les premières valeurs possibles des θk. Pour k > 6, nous pourrons bien évidemment prendre θk = 10-k d'après l'équivalent de la fonction tangente en 0 :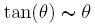 
.
Le tableau ci-dessous donne les premières valeurs à choisir pour θk, à 10-20 près, exprimé en radians :
| k | 10-k | θk = Arctan(10-k) |
|---|---|---|
| 0 | 1 | 0,78539816339744830962 |
| 1 | 0,1 | 0,099668652491162027378 |
| 2 | 0,01 | 0,0099996666866652382063 |
| 3 | 0,001 | 0,00099999966666686666652 |
| 4 | 0,0001 | 0,000099999999666666668667 |
| 5 | 0,00001 | 0,0000099999999996666666667 |
| 6 | 0,000001 | 0,00000099999999999966666667 |
Néanmoins, bien que 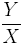soit une valeur approchée de tan(θ), Y et X ne sont guère les valeurs approchées respectives de sin(θ) et de cos(θ) puisqu'il existe un produit de cosinus et de X0 que nous avons laissé de côté depuis le début.
En fait, il suffit d'utiliser les formules peu coûteuses :
.
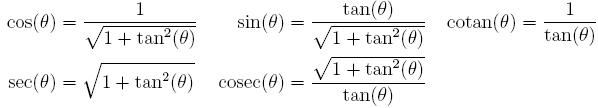Notons enfin que l'algorithme n'est valable que pour des angles θ tels que . Pour les autres angles, on se ramène à cet intervalle à l'aide de relations issues de la symétrie des courbes trigonométriques, comme cos(–θ) = cos(θ) ou sin(π–θ) = sin(θ).
Présentons tout d'abord un pseudo-code de l'algorithme, c'est-à-dire le détail des opérations à effectuer sans syntaxe propre à un langage.
Initialisation des variables utilisées :
si besoin est, en mettant en mémoire la transformation simple finale à appliquer pour obtenir le bon résultat ;Tant que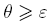 
:
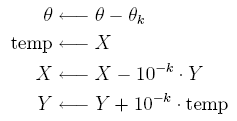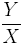., valeur de tan(θ).Il ne reste plus qu'à implémenter ce pseudo-code dans un langage de programmation.
Vous pouvez dès maintenant tester l'algorithme CORDIC que j'ai implémenté en PHP sur TrigoFACILE.
Il vous suffit d'indiquer l'angle en degrés dont vous désirez calculer la tangente dans la case ci-dessous :
↑ Retour au haut de cette page